what container appeared to have the least volume of liquid?

Chapter one. Essential Ideas

1.5 Measurement Doubt, Accurateness, and Precision

Learning Objectives

By the stop of this section, you will be able to:

• Ascertain accuracy and precision
• Distinguish exact and uncertain numbers
• Correctly represent dubiety in quantities using significant figures
• Utilise proper rounding rules to computed quantities

Counting is the only type of measurement that is gratuitous from doubtfulness, provided the number of objects being counted does non alter while the counting procedure is underway. The result of such a counting measurement is an case of an verbal number. If we count eggs in a carton, nosotros know exactly how many eggs the carton contains. The numbers of defined quantities are also verbal. By definition, 1 foot is exactly 12 inches, 1 inch is exactly two.54 centimeters, and 1 gram is exactly 0.001 kilogram. Quantities derived from measurements other than counting, however, are uncertain to varying extents due to practical limitations of the measurement process used.

Significant Figures in Measurement

The numbers of measured quantities, unlike defined or direct counted quantities, are not exact. To measure the volume of liquid in a graduated cylinder, you lot should make a reading at the bottom of the meniscus, the lowest bespeak on the curved surface of the liquid.

Effigy 1. To measure the book of liquid in this graduated cylinder, you must mentally subdivide the distance between the 21 and 22 mL marks into tenths of a milliliter, and then make a reading (estimate) at the bottom of the meniscus.

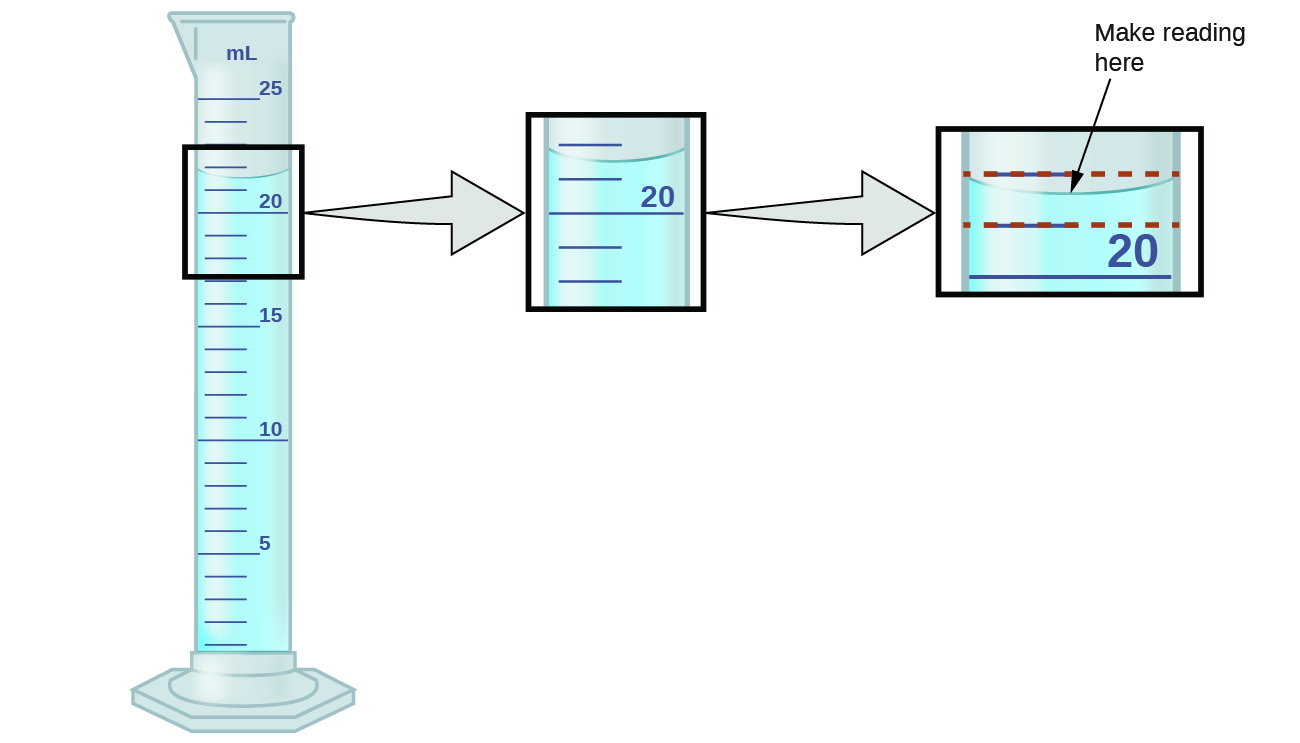
Refer to the illustration in Effigy 1. The bottom of the meniscus in this case clearly lies betwixt the 21 and 22 markings, meaning the liquid volume is certainly greater than 21 mL simply less than 22 mL. The meniscus appears to exist a bit closer to the 22-mL mark than to the 21-mL marking, and so a reasonable guess of the liquid's volume would be 21.six mL. In the number 21.6, then, the digits 2 and 1 are certain, but the 6 is an judge. Some people might estimate the meniscus position to exist equally distant from each of the markings and guess the tenth-place digit as five, while others may think it to exist fifty-fifty closer to the 22-mL mark and approximate this digit to exist 7. Annotation that it would exist pointless to attempt to judge a digit for the hundredths place, given that the tenths-place digit is uncertain. In general, numerical scales such equally the one on this graduated cylinder will permit measurements to i-tenth of the smallest calibration division. The scale in this instance has 1-mL divisions, so volumes may exist measured to the nearest 0.ane mL.

This concept holds true for all measurements, even if you do not actively make an estimate. If you place a quarter on a standard electronic balance, you may obtain a reading of 6.72 1000. The digits 6 and 7 are certain, and the 2 indicates that the mass of the quarter is likely between 6.71 and 6.73 grams. The quarter weighs about vi.72 grams, with a nominal dubiousness in the measurement of ± 0.01 gram. If we weigh the quarter on a more sensitive balance, we may find that its mass is 6.723 g. This ways its mass lies between 6.722 and 6.724 grams, an incertitude of 0.001 gram. Every measurement has some uncertainty, which depends on the device used (and the user'southward power). All of the digits in a measurement, including the uncertain final digit, are called significant figures or significant digits. Note that null may be a measured value; for instance, if you stand on a calibration that shows weight to the nearest pound and it shows "120," then the one (hundreds), 2 (tens) and 0 (ones) are all pregnant (measured) values.

Whenever you lot make a measurement properly, all the digits in the result are meaning. But what if you were analyzing a reported value and trying to decide what is significant and what is not? Well, for starters, all nonzero digits are significant, and it is simply zeros that require some thought. We volition apply the terms "leading," "abaft," and "captive" for the zeros and will consider how to bargain with them.

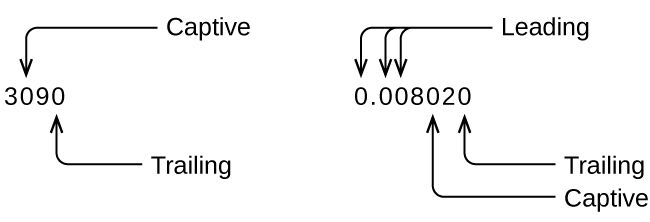
Starting with the commencement nonzero digit on the left, count this digit and all remaining digits to the right. This is the number of significant figures in the measurement unless the last digit is a trailing zero lying to the left of the decimal point.

Convict zeros result from measurement and are therefore e'er significant. Leading zeros, however, are never significant—they only tell u.s. where the decimal point is located.

The leading zeros in this example are not significant. We could utilise exponential notation (equally described in Appendix B) and express the number as 8.32407 × 10^−three; then the number 8.32407 contains all of the significant figures, and 10^−three locates the decimal point.

The number of significant figures is uncertain in a number that ends with a goose egg to the left of the decimal betoken location. The zeros in the measurement 1,300 grams could exist significant or they could only indicate where the decimal indicate is located. The ambiguity can exist resolved with the employ of exponential notation: 1.three × 10³ (ii significant figures), 1.30 × 10³ (iii meaning figures, if the tens place was measured), or i.300 × 10ⁱⁱⁱ (four meaning figures, if the ones place was likewise measured). In cases where only the decimal-formatted number is available, it is prudent to presume that all trailing zeros are not significant.

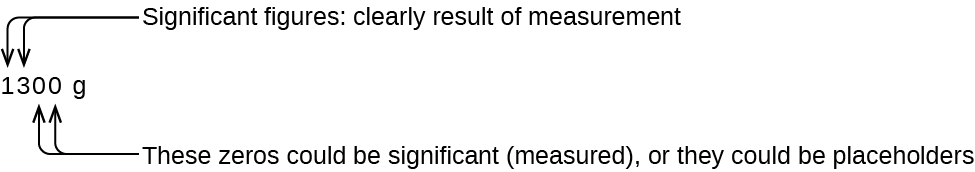
When determining significant figures, be certain to pay attending to reported values and remember about the measurement and pregnant figures in terms of what is reasonable or likely when evaluating whether the value makes sense. For example, the official Jan 2014 census reported the resident population of the US as 317,297,725. Exercise you think the Us population was correctly determined to the reported nine pregnant figures, that is, to the exact number of people? People are constantly being born, dying, or moving into or out of the country, and assumptions are fabricated to account for the large number of people who are not actually counted. Because of these uncertainties, it might be more reasonable to wait that we know the population to within perhaps a 1000000 or so, in which example the population should exist reported every bit three.17 × 10^viii people.

Pregnant Figures in Calculations

A second of import principle of dubiousness is that results calculated from a measurement are at least every bit uncertain as the measurement itself. We must take the dubiety in our measurements into business relationship to avoid misrepresenting the uncertainty in calculated results. 1 fashion to exercise this is to written report the effect of a calculation with the right number of significant figures, which is adamant by the following 3 rules for rounding numbers:

1. When nosotros add or subtract numbers, we should round the event to the same number of decimal places every bit the number with the least number of decimal places (the least precise value in terms of add-on and subtraction).
2. When nosotros multiply or divide numbers, we should round the result to the same number of digits as the number with the least number of significant figures (the least precise value in terms of multiplication and division).
3. If the digit to be dropped (the one immediately to the right of the digit to be retained) is less than 5, we "round down" and leave the retained digit unchanged; if it is more than than 5, we "circular upwardly" and increment the retained digit by i; if the dropped digit is five, we round upwardly or down, whichever yields an fifty-fifty value for the retained digit. (The last part of this dominion may strike you as a bit odd, simply it's based on reliable statistics and is aimed at avoiding whatsoever bias when dropping the digit "5," since it is as shut to both possible values of the retained digit.)

The post-obit examples illustrate the application of this rule in rounding a few dissimilar numbers to three significant figures:

• 0.028675 rounds "up" to 0.0287 (the dropped digit, 7, is greater than 5)
• 18.3384 rounds "down" to 18.three (the dropped digit, 3, is less than 5)
• 6.8752 rounds "up" to 6.88 (the dropped digit is 5, and the retained digit is even)
• 92.85 rounds "down" to 92.8 (the dropped digit is five, and the retained digit is even)

Let's work through these rules with a few examples.

Example 1

Rounding Numbers
Round the following to the indicated number of significant figures:

(a) 31.57 (to 2 significant figures)

(b) viii.1649 (to three significant figures)

(c) 0.051065 (to 4 significant figures)

(d) 0.90275 (to four significant figures)

Solution
(a) 31.57 rounds "up" to 32 (the dropped digit is 5, and the retained digit is even)

(b) eight.1649 rounds "down" to 8.16 (the dropped digit, 4, is less than 5)

(c) 0.051065 rounds "down" to 0.05106 (the dropped digit is 5, and the retained digit is fifty-fifty)

(d) 0.90275 rounds "up" to 0.9028 (the dropped digit is five, and the retained digit is even)

Bank check Your Learning
Round the following to the indicated number of meaning figures:

(a) 0.424 (to ii significant figures)

(b) 0.0038661 (to three significant figures)

(c) 421.25 (to 4 significant figures)

(d) 28,683.five (to five meaning figures)

Reply:

(a) 0.42; (b) 0.00387; (c) 421.2; (d) 28,684

Example 2

Addition and Subtraction with Significant Figures
Dominion: When nosotros add or decrease numbers, we should round the result to the same number of decimal places as the number with the least number of decimal places (i.e., the least precise value in terms of addition and subtraction).

(a) Add together 1.0023 yard and 4.383 1000.

(b) Subtract 421.23 yard from 486 g.

Solution

(a) [latex]\displaystyle \begin{array}{r}1.0023 \text{grand} \\ +4.383 \;\;\text{yard} \\ \hline 5.3853 \text{g} \finish{array}[/latex]

Answer is 5.385 g (round to the thousandths place; iii decimal places)

(b) [latex]\displaystyle \begin{array}{r}486 \;\;\;\;\; \text{g} \\ -421.23 \text{g} \\ \hline 64.77 \text{grand} \stop{array}[/latex]

Respond is 65 thousand (round to the ones place; no decimal places)

Check Your Learning
(a) Add two.334 mL and 0.31 mL.

(b) Subtract 55.8752 m from 56.533 grand.

Reply:

(a) two.64 mL; (b) 0.658 chiliad

Example 3

Multiplication and Division with Meaning Figures
Rule: When we multiply or divide numbers, nosotros should round the consequence to the same number of digits as the number with the to the lowest degree number of meaning figures (the to the lowest degree precise value in terms of multiplication and division).

(a) Multiply 0.6238 cm by 6.6 cm.

(b) Divide 421.23 g by 486 mL.

Solution

(a) [latex]0.6238 \text{ cm} \times 6.vi \text{ cm} = iv.11708 \text{ cm}^2 \rightarrow \text{issue is 4.1} \text{cm}^two \text{(round to ii significant figures)} \\[0.75em] \text{four meaning figures} \times \text{two pregnant figures} \rightarrow \text{two significant figures answer}[/latex]

(b) [latex]\frac{421.23 \text{g}}{486 \text{mL}}=0.86728 \dots \text{g/mL} \rightarrow \text{effect is 0.867 g/mL (round to 3 meaning figures)} \\[0.75em] \frac{\text{five significant figures}}{\text{three significant figures}} \rightarrow \text{3 significant figures answer}[/latex]

Check Your Learning
(a) Multiply 2.334 cm and 0.320 cm.

(b) Divide 55.8752 m by 56.53 s.

Answer:

(a) 0.747 cm² (b) 0.9884 1000/s

In the midst of all these technicalities, it is important to keep in mind the reason why nosotros use meaning figures and rounding rules—to correctly represent the certainty of the values nosotros report and to ensure that a calculated consequence is not represented every bit existence more certain than the least sure value used in the calculation.

Example 4

Calculation with Pregnant Figures
1 mutual bathtub is 13.44 dm long, 5.920 dm wide, and 2.54 dm deep. Assume that the tub is rectangular and calculate its approximate volume in liters.

Solution

[latex]\begin{assortment}{r @{{}={}} l}Five & l \times due west\times d \\ & xiii.44 \text{ dm} \times 5.920 \text{ dm} \times 2.54 \text{ dm} \\ & 202.09459\dots \text{ dm}^three \text{(value from calculator)} \\ & 202 \text{ dm}^3,\;\text{or}\;202\text{ 50 (answer rounded to three significant figures)} \finish{array}[/latex]

Cheque Your Learning
What is the density of a liquid with a mass of 31.1415 g and a volume of 30.13 cm³?

Example 5

Experimental Determination of Density Using Water Displacement
A piece of rebar is weighed and so submerged in a graduated cylinder partially filled with water, with results equally shown.

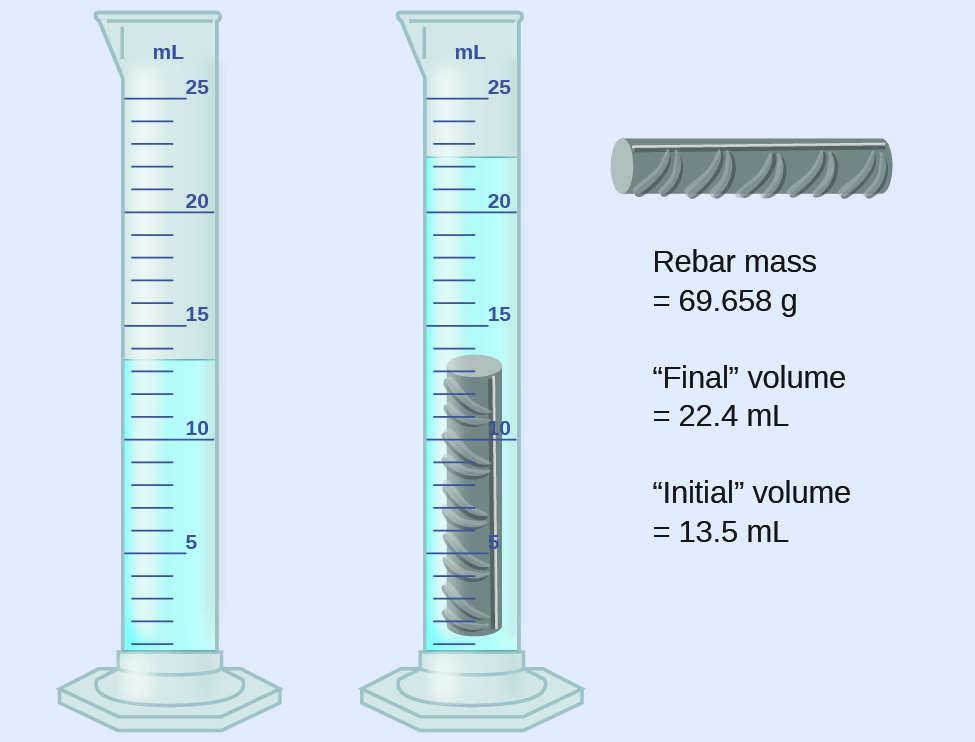
(a) Use these values to decide the density of this piece of rebar.

(b) Rebar is mostly iron. Does your event in (a) support this statement? How?

Solution
The book of the piece of rebar is equal to the volume of the water displaced:

[latex]\text{volume} = 22.4 \text{mL} - xiii.v \text{mL} = 8.9 \text{mL} = viii.ix \text{cm}^3[/latex]

(rounded to the nearest 0.1 mL, per the rule for improver and subtraction)

The density is the mass-to-volume ratio:

[latex]\text{density} = \frac{\text{mass}}{\text{book}} = \frac{69.658 \text{chiliad}}{8.ix \text{cm}^3} = 7.8 \text{g/cm}^iii[/latex]

(rounded to two significant figures, per the rule for multiplication and partition)

From Table 4 in Chapter 1.4 Measurements, the density of iron is 7.ix g/cm³, very shut to that of rebar, which lends some support to the fact that rebar is generally iron.

Check Your Learning
An irregularly shaped piece of a shiny yellow textile is weighed and and then submerged in a graduated cylinder, with results equally shown.

(a) Use these values to decide the density of this material.

(b) Practice yous have whatsoever reasonable guesses as to the identity of this textile? Explain your reasoning.

Answer:

(a) 19 one thousand/cmⁱⁱⁱ; (b) Information technology is likely golden; the correct appearance for gold and very shut to the density given for gold in Table iv in Chapter 1.iv Measurements.

Accuracy and Precision

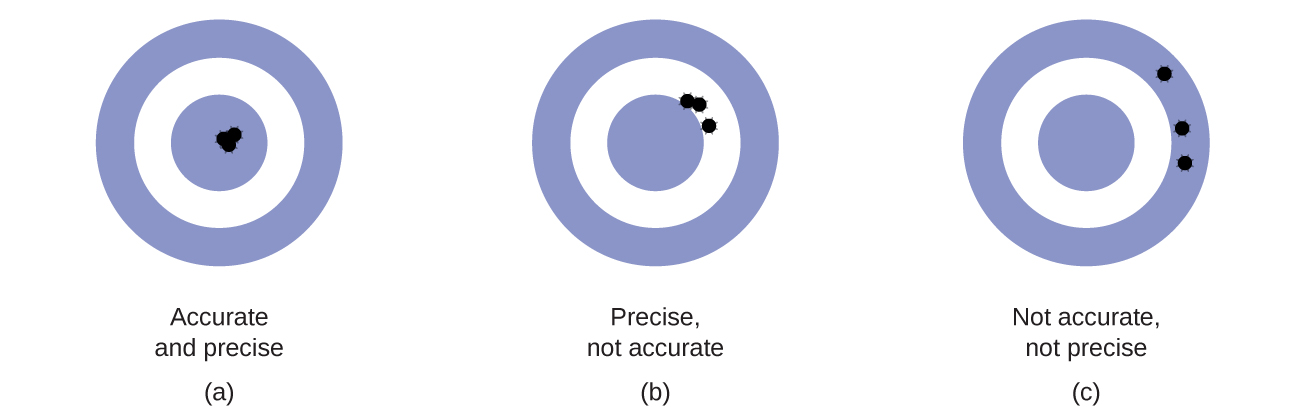
Scientists typically make repeated measurements of a quantity to ensure the quality of their findings and to know both the precision and the accurateness of their results. Measurements are said to be precise if they yield very similar results when repeated in the same manner. A measurement is considered accurate if it yields a result that is very close to the true or accepted value. Precise values concur with each other; accurate values concord with a truthful value. These characterizations can be extended to other contexts, such as the results of an archery competition (Figure 2).

Figure 2. (a) These arrows are close to both the bull'southward eye and one some other, and then they are both authentic and precise. (b) These arrows are close to one some other but not on target, so they are precise but not authentic. (c) These arrows are neither on target nor close to ane another, and so they are neither authentic nor precise.

Suppose a quality control chemist at a pharmaceutical visitor is tasked with checking the accuracy and precision of iii different machines that are meant to dispense ten ounces (296 mL) of cough syrup into storage bottles. She gain to use each motorcar to fill five bottles and and so carefully determines the bodily book dispensed, obtaining the results tabulated in Table v.

Dispenser #ane	Dispenser #2	Dispenser #3
283.3	298.3	296.1
284.1	294.2	295.9
283.nine	296.0	296.1
284.0	297.eight	296.0
284.1	293.ix	296.one
Table 5. Book (mL) of Cough Medicine Delivered by ten-oz (296 mL) Dispensers

Because these results, she will written report that dispenser #1 is precise (values all close to ane some other, within a few tenths of a milliliter) but non accurate (none of the values are close to the target value of 296 mL, each existence more than than x mL besides low). Results for dispenser #ii represent improved accuracy (each volume is less than 3 mL away from 296 mL) but worse precision (volumes vary by more than iv mL). Finally, she can written report that dispenser #3 is working well, dispensing cough syrup both accurately (all volumes within 0.1 mL of the target volume) and precisely (volumes differing from each other past no more than 0.ii mL).

Primal Concepts and Summary

Quantities tin can be exact or measured. Measured quantities have an associated uncertainty that is represented by the number of significant figures in the measurement. The uncertainty of a calculated value depends on the uncertainties in the values used in the adding and is reflected in how the value is rounded. Measured values tin be accurate (shut to the true value) and/or precise (showing little variation when measured repeatedly).

Chemistry End of Affiliate Exercises

1. Express each of the following numbers in scientific notation with correct significant figures:

   (a) 711.0

   (b) 0.239

   (c) 90743

   (d) 134.2

   (e) 0.05499

   (f) 10000.0

   (yard) 0.000000738592

2. Express each of the post-obit numbers in exponential notation with correct significant figures:

   (a) 704

   (b) 0.03344

   (c) 547.9

   (d) 22086

   (e) 1000.00

   (f) 0.0000000651

   (g) 0.007157

3. Indicate whether each of the following can exist adamant exactly or must be measured with some degree of doubt:

   (a) the number of eggs in a basket

   (b) the mass of a dozen eggs

   (c) the number of gallons of gasoline necessary to fill an automobile gas tank

   (d) the number of cm in 2 yard

   (e) the mass of a textbook

   (f) the fourth dimension required to drive from San Francisco to Kansas City at an boilerplate speed of 53 mi/h

4. Indicate whether each of the following can be determined exactly or must be measured with some degree of uncertainty:

   (a) the number of seconds in an hour

   (b) the number of pages in this book

   (c) the number of grams in your weight

   (d) the number of grams in 3 kilograms

   (due east) the volume of water you drink in one day

   (f) the distance from San Francisco to Kansas City

5. How many significant figures are contained in each of the following measurements?

   (a) 38.seven k

   (b) 2 × x¹⁸ m

   (c) iii,486,002 kg

   (d) 9.74150 × 10^−four J

   (e) 0.0613 cm³

   (f) 17.0 kg

   (one thousand) 0.01400 g/mL

6. How many significant figures are contained in each of the following measurements?

   (a) 53 cm

   (b) 2.05 × 10⁸ m

   (c) 86,002 J

   (d) nine.740 × ten⁴ grand/southward

   (e) ten.0613 1000³

   (f) 0.17 g/mL

   (g) 0.88400 s

7. The following quantities were reported on the labels of commercial products. Decide the number of pregnant figures in each.

   (a) 0.0055 1000 active ingredients

   (b) 12 tablets

   (c) 3% hydrogen peroxide

   (d) v.5 ounces

   (due east) 473 mL

   (f) 1.75% bismuth

   (g) 0.001% phosphoric acid

   (h) 99.80% inert ingredients

8. Round off each of the post-obit numbers to two significant figures:

   (a) 0.436

   (b) 9.000

   (c) 27.ii

   (d) 135

   (e) 1.497 × 10⁻³

   (f) 0.445

9. Round off each of the following numbers to two significant figures:

   (a) 517

   (b) 86.3

   (c) half-dozen.382 × ten³

   (d) 5.0008

   (e) 22.497

   (f) 0.885

10. Perform the following calculations and report each respond with the right number of significant figures.

    (a) 628 × 342

    (b) (5.63 × 10ⁱⁱ) × (7.four × ten³)

    (c) [latex]\frac{28.0}{13.483}[/latex]

    (d) 8119 × 0.000023

    (due east) 14.98 + 27,340 + 84.7593

    (f) 42.7 + 0.259

11. Perform the following calculations and written report each answer with the right number of significant figures.

    (a) 62.eight × 34

    (b) 0.147 + 0.0066 + 0.012

    (c) 38 × 95 × 1.792

    (d) fifteen – 0.xv – 0.6155

    (e) [latex]8.78 \times (\frac{0.0500}{0.478})[/latex]

    (f) 140 + 7.68 + 0.014

    (k) 28.7 – 0.0483

    (h) [latex]\frac{(88.5-87.57)}{45.thirteen}[/latex]

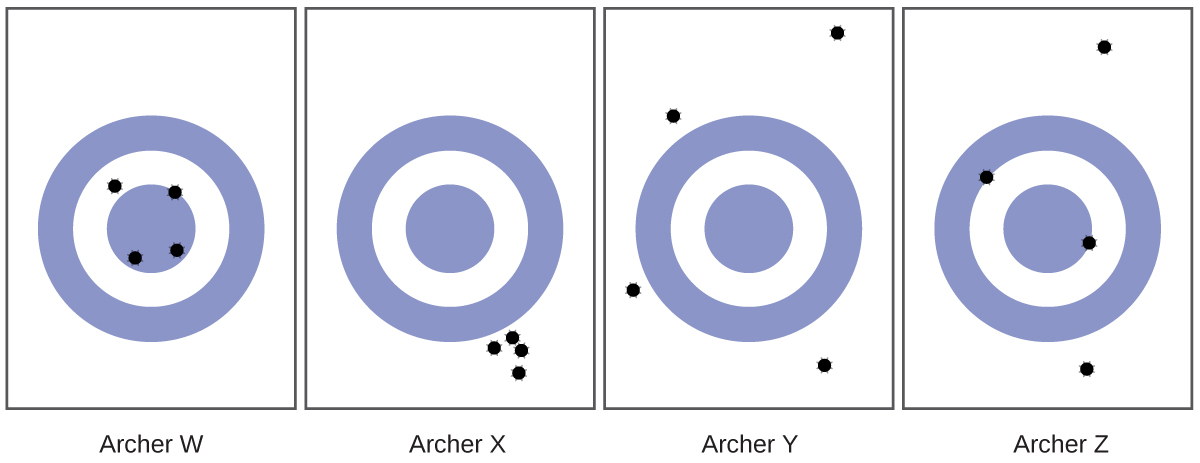
12. Consider the results of the archery contest shown in this figure.

    (a) Which archer is most precise?

    (b) Which archer is most accurate?

    (c) Who is both least precise and to the lowest degree authentic?

    

13. Allocate the following sets of measurements as authentic, precise, both, or neither.

    (a) Checking for consistency in the weight of chocolate fleck cookies: 17.27 g, 13.05 g, xix.46 g, xvi.92 yard

    (b) Testing the volume of a batch of 25-mL pipettes: 27.02 mL, 26.99 mL, 26.97 mL, 27.01 mL

    (c) Determining the purity of gold: 99.9999%, 99.9998%, 99.9998%, 99.9999%

Glossary

accuracy

how closely a measurement aligns with a correct value

verbal number

number derived by counting or by definition

precision

how closely a measurement matches the aforementioned measurement when repeated

rounding

procedure used to ensure that calculated results properly reflect the uncertainty in the measurements used in the calculation

pregnant figures

(also, significant digits) all of the measured digits in a decision, including the uncertain final digit

dubiousness

estimate of amount by which measurement differs from true value

Solutions

Answers for Chemistry End of Chapter Exercises

two. (a) 7.04 × 10ⁱⁱ; (b) iii.344 × ten^−two; (c) five.479 × 10²; (d) 2.2086 × 10⁴; (east) ane.00000 × 10³; (f) 6.51 × 10⁻⁸; (g) seven.157 × 10⁻³

iv. (a) exact; (b) verbal; (c) uncertain; (d) exact; (e) uncertain; (f) uncertain

6. (a) 2; (b) three; (c) five; (d) 4; (e) 6; (f) 2; (g) five

eight. (a) 0.44; (b) 9.0; (c) 27; (d) 140; (e) 1.five × 10⁻ⁱⁱⁱ; (f) 0.44

10. (a) 2.15 × x^v; (b) iv.2 × 10^{half dozen}; (c) 2.08; (d) 0.xix; (e) 27,440; (f) 43.0

12. (a) Archer X; (b) Archer W; (c) Archer Y

loartheight.blogspot.com

Source: https://opentextbc.ca/chemistry/chapter/measurement-uncertainty-accuracy-and-precision/

Share this post